Lagrangeove točke posebni su položaji u sustavu Sunce i Zemlja gdje se gravitacijska polja oba tijela zbrajaju tako da je rezultantna sila na malo treće tijelo vrlo mala; zato letjelica ondje može održavati stabilnu putanju uz minimalne korekcije. Zbog toga su Lagrangeove točke ključna infrastruktura za astronomiju i planiranje budućih svemirskih misija.
Astronomi često rabe parsek; to je 3,26 svjetlosnih godina. U ovom tekstu udaljenosti navodimo u kilometrima. Imperijalne ekvivalente dodajemo u zagradama.
Stabilne Lagrangeove točke L4 i L5
Polazište je Newtonova ideja da ista sila koja jabuku privlači prema tlu drži i Mjesec na nebu; dovoljno je da tijelo ima pravu brzinu. Kada promatramo sustav s dvama masivnim tijelima, primjerice Sunce i Zemlju, njihova se gravitacijska polja vektorski zbrajaju; u pojedinim položajima ukupna sila na treće, vrlo malo tijelo gotovo je jednaka nuli. Na takvim mjestima to tijelo može dugotrajno održavati orbitu uz minimalne korekcije. Te su točke nazvane po Josephu Louisu Lagrangeu, a Leonhard Euler ranije je matematički opisao tri takva rješenja u sklopu ograničenog problema triju tijela.
U praksi razlikujemo pet Lagrangeovih položaja, L1 do L5. Dva se posebno izdvajaju jer su, uz povoljan omjer masa, dinamički stabilni; to su L4 i L5. Smješteni su oko 60 stupnjeva ispred i 60 stupnjeva iza planeta na njegovoj stazi oko Sunca. Manja tijela ondje ne miruju; opisuju male zatvorene putanje oko tih točaka i blago se osciliraju. Asteroidi u takvim orbitama mogu opstati milijunima godina, osobito u sustavima poput Sunca i Jupitera; sitna prašina zbog Sunčeva zračenja ne zadržava se dugotrajno.
Stabilnost takvih dinamički stabilnih položaja najlakše je uočiti kod Jupitera. Njegovi Trojanci u L4 i L5 čine prirodni laboratorij stabilnosti. Lucy je na putu prema tim populacijama kako bi istražila njihovo podrijetlo i građu; dugotrajna prisutnost Trojanaca pokazuje da L4 i L5 ostaju stabilni na geološkim skalama vremena.
Zašto je Jupiter najbogatiji Trojancima? Ključ je razmjer. Zbog velikog udjela Jupitera u ukupnoj masi sustava Sunce i Jupiter oko točaka L4 i L5 stvara se šire područje dinamičke stabilnosti; blizina glavnog asteroidnog pojasa dodatno omogućuje stalan priljev malih tijela u te regije. Potvrđeni Trojanci poznati su kod Jupitera, Neptuna i Marsa; Zemlja ima dva potvrđena objekta. Za Veneru, Uran i Saturn postoje kandidati ili kratkotrajno vezane konfiguracije, no dugoročna stabilnost zasad nije potvrđena; Merkur nema poznate Trojance.
Ovdje je korisno uvesti pojam baricentra. Planeti ne kruže oko središta Sunca nego oko zajedničkog središta mase sustava. Kod unutarnjih planeta baricentar se nalazi unutar Sunčeva tijela; u sustavu Sunce i Jupiter leži malo izvan Sunčeve površine. Neovisno o njegovu položaju, točke L4 i L5 postoje, a mala tijela u njihovoj blizini mogu uspostaviti dugotrajno stabilne orbite. Zbog toga se naziv ‘Trojanci’ danas koristi i za trojanske asteroide drugih planeta, ne samo Jupitera.
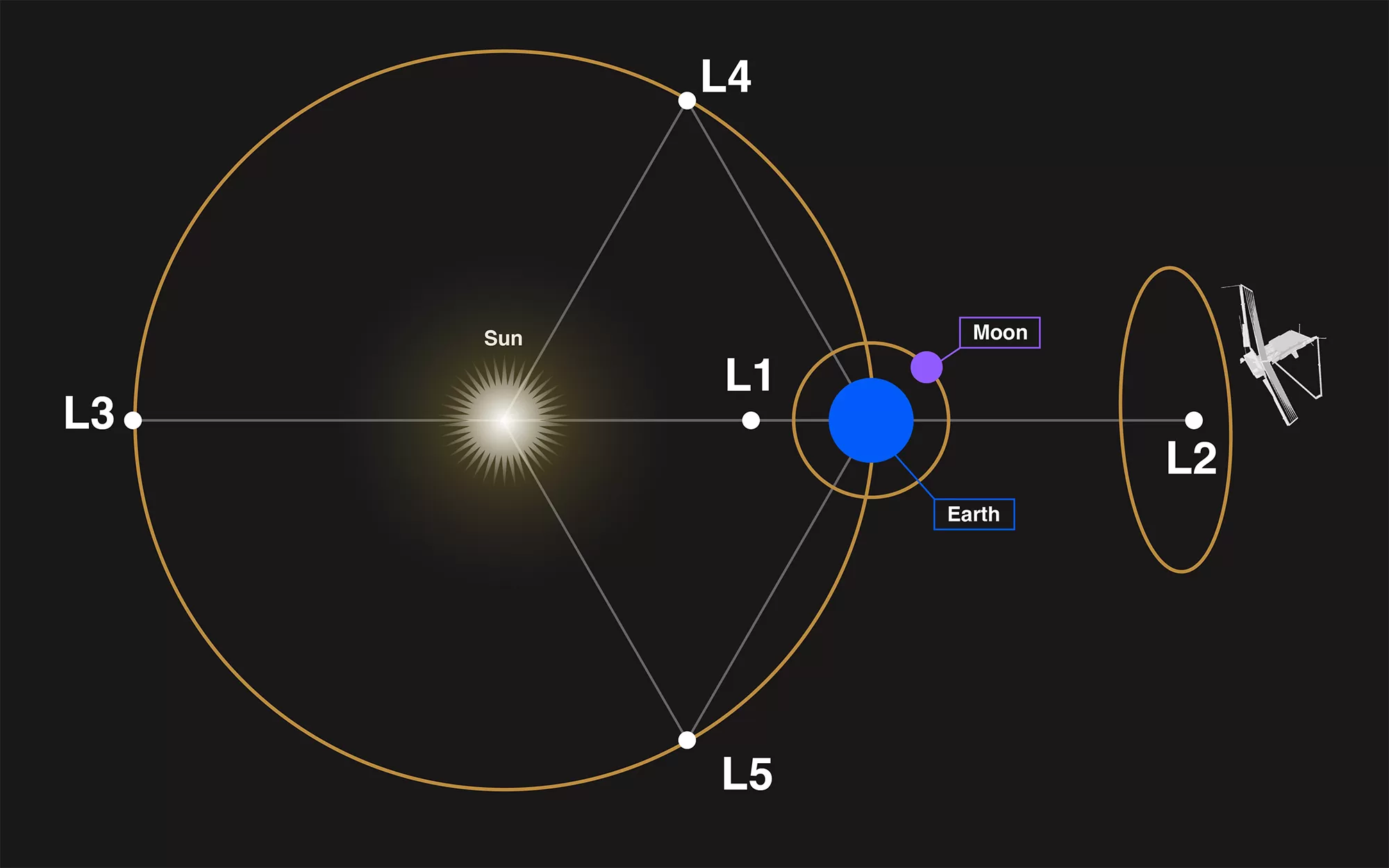
L1 i L2: Lagrangeove točke u službi astronomije
Za promatranje Sunca i dubokog svemira presudni su položaji na liniji Sunce–Zemlja. L1 se nalazi približno 1,5 milijuna km od središta Zemlje prema Suncu. U tom položaju kombinirani gravitacijski utjecaj Sunca i Zemlje omogućuje da letjelica obilazi Sunce istim ritmom kao i Zemlja; ne “bježi” naprijed i ne zaostaje.
Važna napomena. L1 nije apsolutno stabilna točka; mali odmak s vremenom raste. Ipak, boravak u blizini zahtijeva tek povremeno održavanje putanje s vrlo malim impulsima. Zbog toga je L1 idealna za sonde koje stalno prate Sunčev vjetar, erupcije i međuplanetarno okruženje te pravovremeno upozoravaju na promjene svemirskog vremena. Povremeno se razmatra i geoinženjerska ideja postavljanja tankog zaslona ili oblaka prašine u L1 kako bi se neznatno smanjio dotok Sunčeve svjetlosti na Zemlju; koncept je fizički zamisliv, ali operativna, pravna i politička izvedivost ostaje vrlo upitna.
Na strani suprotnoj od Sunca nalazi se L2. Ondje se Zemljina gravitacija pridodaje Sunčevoj tako da se efektivna kutna brzina objekta poveća i uskladi sa Zemljinom; objekt oko Sunca obilazi za jednu godinu iako je dalje od Sunca od Zemlje. Prednosti su praktične i velike.
U okolini L2 svemirski teleskopi mogu stalno promatrati duboki svemir, dok Sunce, Zemlja i Mjesec ostaju u približno istom smjeru iza instrumenta; toplinski uvjeti su stabilni, a razina zalutale svjetlosti manja. Svemirski teleskop James Webb radi upravo u tom okruženju; ne nalazi se točno u geometrijskoj točki L2 nego prati stabilnu halo-putanju u njezinoj blizini i povremeno korigira putanju s malo pogonskog sredstva.
U istom je susjedstvu i misija Euclid; u budućnosti će mu se pridružiti i Nancy Grace Roman Space Telescope. To su primjeri kako Lagrangeove točke pretvaraju složenu gravitacijsku dinamiku u pouzdanu radnu platformu za preciznu astronomiju.
Slika nije potpuna bez L3. Ta se točka nalazi točno s druge strane Sunca u odnosu na Zemlju; često se spominje u nagađanjima o “skrivenom planetu”, no višegodišnja opažanja brojnih međuplanetarnih misija nisu otkrila nikakav objekt planetarne veličine u tom položaju.
Važno je napomenuti da Lagrangeove točke ne pripadaju samo parovima Sunce i planet; svaki par masivnih tijela ima vlastite točke, pa tako i sustav Zemlja i Mjesec. U tom sustavu L1 se često navodi kao pogodno logističko čvorište za sastavljanje i opskrbu većih letjelica; odatle je lakše kretati prema različitim odredištima jer su potrebne promjene brzine, tzv. delta v, manje nego pri polijetanju s površine Zemlje.
Lagrangeove točke nastaju jer se gravitacijska polja dvaju masivnih tijela zbrajaju tako da je u određenim položajima rezultantna sila na treće, vrlo malo tijelo gotovo jednaka nuli. Zato Lagrangeove točke nisu egzotični kuriozitet, nego stvarna infrastruktura za znanost i istraživanje. Kratko rečeno, Lagrangeove točke pretvaraju gravitaciju u koristan alat.
Ivan je novinar i autor koji piše o znanosti, svemiru i povijesti. Gostuje kao stručni sugovornik na Science Discovery i History Channelu te piše za Večernji list. Osnivač je Kozmos.hr, prvog hrvatskog portala posvećenog popularizaciji znanosti.









